In nuclear medicine applications, image reconstruction from radio-nuclide emissions is known as computed tomography (CT) and its purpose is the localisation of the emission hot spots. Various image reconstruction algorithms exist, and their applicability depends, among other factors, on the type of scanning apparatus (PET, PEM, SPECT, Compton camera) and the type of emission nucleide (e.g. positron emission or single gamma). Important concepts in medical imaging are the field of view (FOV), which is the space onto which the image is reconstructed and the projection data, which reflects how the emission radiation is projected onto the detector (i.e. the measured data).

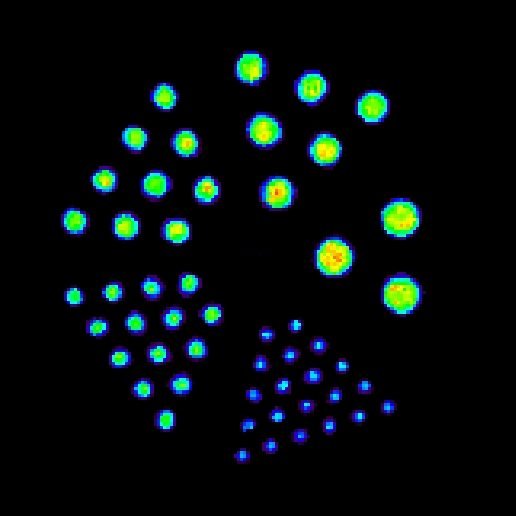
Figure 1. Derenzo Phantom.

With PET and PEM, by connecting the two hit positions for each event, we can establish the line-of-response (LOR) on which the source of the emission lies, whereas with Compton cameras, the emission source is located on the surface of the Compton cone for each event. For the VIP project, where the proposed detector designs (PET, PEM and Compton camera) have a large number of finely segmented data-channels, image reconstruction is a challenging task. Simple backprojection, the most basic approach, where the detector data is projected back onto the FOV, results in a blurred image, so more complicated algorithms are often needed. Conventional algorithms like Filtered Back-Projection (FBP) and Ordered Subset Expectation Maximization (OSEM) are straightforward to use for PET scannes, but for PEM and - especially - Compton cameras have disadvantages.

With FBP, a Fourier transform, a frequency filter and, subsequently, an inverse Fourier transform are applied to the data before doing back-projection. The main drawback of FBP is that it requires a detector with an angular coverage of at least 180 degrees and hence cannot be used for PEM and Compton gamma cameras without producing artifacts in the final image. OSEM is an iterative algorithm, where an image estimate is forward projected onto the detector and after comparing the projected data with the real measured data, a cost function is used to update the image estimate. The main problem with OSEM for a Compton gamma camera with a large number of channels is that it requires an impractical large memory and CPU-time consumption since the total number of detector bins in the system matrix depends on all possible combinations of all channels in the two Compton camera detector planes. A list mode implementation of OSEM (LM-OSEM), might reduce this disadvantage but still there are various issues involved in optimizing the algorithm, such as the search algorithm for finding the FOV bins that lie on the Compton cone (or the LOR in the case of PET and PEM), and to what extent potential tracks should be weighted with their corresponding cross-section. As an alternative, the Origin Ensemble (OE) algorithm can be used, which is based on a stochastic approach. Here, iteratively, random positions are assigned in the FOV for the Compton cones or LORs, with probabilities depending on the density of positions in each of the FOV bins. Due to the stochastic nature of the algorithm, various trial runs have to be executed and the final result is an average of these. Also, to counteract the finite spatial resolution of the detectors, a additional resolution recovery mechanism has to be added to the mechanism. To evaluate these image reconstruction algorithms, they should be tested on various phantom sources (such as the Derenzo phantom shown in the figure 1) where the results should be compared by using various image quality criteria.